In part 1 we defined our game building blocks and mechanics and observed the exponential growth of possible game states and level complexity. In part 2 we found a way to verify our levels as to guarantee the 3 basic rules of our game (no dead ends, with and without max-combo, a no-combo solution can’t be shorter than a combo one) and we assigned a 3-star rating system for our correct levels.
Our final goal though is to create fair, fun and interesting challenges, and a correct level only satisfies the fairness constraint so we are going to try and define additional rules to improve our rating system and highlight the fun and interesting components of a level.
These rules must represent the feedback from playtesting sample levels both by the designer and players with different levels of experience in videogames. They must try to define “fun” and ‘interesting” while staying consistent with the communication we are creating between the game and the player through our mechanics and levels sequence. Let’s see an example of the content of this communication.
Silent tutorial, natural learning
Skiddy has a total of 12 worlds. The first contains only red Skiddies. The next 4 worlds present a single new object each. Following worlds will combine these objects, creating even more complex puzzles.
The first few levels of each world act as a “silent tutorial” to guide players toward a natural learning of each new object’s properties, understanding through playing.
We can see this in the progression of the first 4 levels of World 1:
Level 1 - The minimum playable level: 2 Skiddies to get max combo, an empty plane and one exit | Level 2 - The plane is not a rectangle, there can be static obstacles | Level 3 - There can be more than one exit.Vertical symmetry makes left and right solutions equivalent | Level 4 - We can’t clear single Skiddies but we can still break the max-combo with 2 double combos |
These sequence of 4 simple levels subtly teaches a lot of game mechanics, but we can go one level further and analyze the moves we are allowed to make in a couple of easy levels to see how the “natural learning” idea works within a single board.
Level 1-1, we learn how to get medals and break the combo
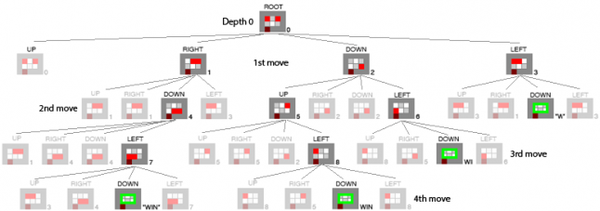
We can’t move up, so we immediately reduce the choice to three directions to limit a beginner’s confusion. After noticing the bottom exit, usually our first instinct is to go down, in this way we clear 1 Skiddy in 1 move. We are left with another lonely one to bounce around and clear the level in at least 2 more moves. We get no medals, but we learn that it’s ok to clear Skiddies one by one. Now we want to get some medals so we try again, doing something different. If we move either left or right, we get the 2 Skiddies stuck together and in this level, there is no way of separating them. Whichever way we move now we will end up with a combo. On the left side, we can go down and clear the level in only 2 moves. This is the minimum and will net us all 3 medals. On the right side, we can either go down-left-down or back left and down, so we clear the level in 4 or 3 moves (typically 4 because on first instinct we generally tend to not backtrack). We learn the difference between combo only (1 medal) and combo in minimum moves (3 medals).
This level also shows how a simple change creates problematic results.
If we move the bottom exit to the middle, we change two things:
There would be no way to break the combo
The only way for the player to learn about the importance of minimum move would be a frustrating ping-pong left and right
Level 1-1 is a simple but comprehensive example of what we learned from our first playtest sessions and helps us defined some positive and negative characteristic of a level.
Positive:
It’s my choice to break the combo. Until all same-color Skiddies are in the level I must be able to get the max combo no matter how I moved before
It’s easy to break the combo if I don’t pay attention. It’s rewarding to focus on my moves
Level layouts, symmetry and block placement have a meaningful purpose
Negative:
Getting the max combo in less moves than it takes to break it reduces the challenge
Levels that are easy to solve just randomly moving around are boring
Correct levels with a feeling of random or unbalanced block placement are not interesting or visually confusing
Lets’ analyze and try to implement point no.1. in our editor.
1 Until all same-color Skiddies are in the level I must be able to get the max combo
To clarify this situation, here’s an example of a level where we break the max combo:

The perfect solution for this level is Down, Left, Down. Starting by moving left we clear the yellow Skiddies in a combo but then it’s impossible to get the red ones in a position that will not break theirs. Even not willingly breaking any color combo, the max combo is now impossible.
While play-testing this became subconsciously expected and felt almost as important as not having dead ends so we decided that it was a necessary condition to get at least 3 stars in our rating system.
To track this, first we define a method (CheckCanCombo) to check if the level state related to a node can still lead to a max combo:
//this class contains all information related to our level game board. //we can unpack all this information from the Node.Value field and recreate //any state while traversing our tree Class Board { … Int NumR; //hold the initial count of red skiddies in this level List <Blocks> Moveables; //moveable blocks in this level //(colored skiddies, crates, ice blocks, etc..) //checks if from this node we can still reach the max combo //returns 0 if can combo, 2 if cannot combo (1 is reserved for later) public int CheckCanCombo() { if (NumR > 0) { int countreds = 0; //count each color skiddy foreach (Block b in Moveables) { if(b.IsType(RedSkiddy)) { countreds++; } //if a color has less than all items, it cannot lead to a combo, //0 means we can still get a combo for this color or the last block for this //color was cleared. If it’s the last one, the node will be excluded in the //final check because the related node State is not set to MaxCombo if (countreds > 0 && countreds != NumR) { return 2; } else return 0; } } … }
Then we add a field (CanCombo) to our node class (defined in part 1 and 2) to track the result.
// A node contains information about board configuration and relations to other nodes class Node { int Value; //encodes our pieces’ layout and board score NodeState State; //max-combo, ok or dead-end? Node[4] Child; //the states originating form the next 4 moves int Index; //generating move(none, up, right, down, left) // -1 0 1 2 3 Node Parent; //state before last move, used to traverse our solution int Depth; //how many moves it took to reach this node int CanCombo; //tracks if the max combo is still reachable from this node //0 can, 2 cannot combo (1 is reserved for later) }
Our root is created with CanCombo = 0 as anyway all blocks are available, then whenever we create a child node from a parent node that can still reach the combo, we perform the check. The first time that we reach a node that breaks the combo, we can save the move sequence so the editor can show us where it breaks.
//creation from an existing node Node node = new Node(value) { Value = value; State = DeadEnd //we do not know if we can reach a solution Parent = CurrentNode; //set the parent for solution traversal Index = index; //we track the originating move Depth = currentNode.Depth + 1; if (CurrentNode.CanCombo < 2) { //only if parent can reach the max combo node.CanCombo = board.CheckCanCombo(); } else { //save the move sequence so we can see it in the editor Board.FirstBreaker = GetFirstBreakerSolution(currentNode); } }
Then we define a method to check if at some point the combo was broken.
//We enumerate through all our unique nodes and check if a node that could still lead //to the max combo (CanCombo == 0) didn’t actually lead to it (State != MaxCombo) public bool BreakComboCheck() { foreach (Node n in Uniques) { if (n.CanCombo == 0) { if (!n.State == NodeState.MaxCombo) return false; } } return true; }
And at the end of our rating check, we can add this after the DeadEnd search, together with the other conditions to get our 3 stars.
… Rating = 0; if (!HasDeadEnds()) { Rating = 1; bool comboUnbroken = BreakComboCheck(); if (noCombo && withCombo) { Rating = 2; if (comboUnbroken) { if (Perfect == Moves) { Rating = 3; … } …
Thanks to the previous state propagation, this important rule was fairly easy to implement, we can move to point no.2.
2 - It’s easy to break the combo if I don’t pay attention. It’s rewarding to focus on my moves
What this means in practice is that it must never take more moves to clear a single Skiddy (or more than one but not all if we have more than 2) from one color group than it takes to get the combo for that group (as we saw in level 1-1). Let’s clarify with a negative example:





































