In part 1 we defined our simple game building blocks and mechanics and observed that even simple levels could quickly generate complexity due to the exponential growth of possible game states. Since it’s important to guarantee that each level is at least correct and solvable according to our rules, we will try to define a way to verify all these states in our generator. We also tried to implement our game states relationship as a standard breadth-first tree and observed that:

This gives us some ideas on how we can revise this tree to improve our analysis.

Let’s review the rules of correctness for a level, according to the 3 medals that can be earned by the player:

We can define a preliminary level rating, from 0 to 3 stars, depending on how many of the above constraints we respect. Each constraint is checked only if the previous one has a positive result, otherwise, the level is discarded (not really but we will see this later).

Only levels rated 3 stars are suitable for the final game set.

Strategy refinement, “reversing” the tree

With all our previous considerations we can determine that a node doesn’t really care about his 4 children, most of its attention is focused on his parent nodes.

So let’s remove the child nodes but keep the parent node. We also add a Depth field that will be useful for solution length tracking.

// A node contains information about board configuration and relations to other nodes
class Node {
      int Value;       //encodes our pieces’ layout and board score
      NodeState State; //max-combo, ok or dead-end?
      Node[4] Child;   //the states originating from the next 4 moves
      int Index;       //generating move (none, up, right, down, left) 
                       //                 -1     0   1      2     3
      Node Parent;     //state before last move, used to traverse our solution
      Int Depth;       //how many moves it took to reach this node
}

As for each new node we need to make sure there is no pre-existing duplicate node, we can supplement our tree class with a separate Dictionary (which should benefit from retrieval-by-key speed close to O(1) as it’s implemented as a Generic type of Hash Table) that can retrieve our node base on the integer encoded value. In the end, this will contain only unique states.

//in our tree class
Dictionary <int, Node> uniqueNodes = new Dictionary();

We start from an existing root state, which is unique, let’s initialize our node and add it to the list:

//create a new node from a value generated by some external method
Root = new Node(value) {
      Value = value;
      State = DeadEnd     //we do not know if we can reach a solution yet
      Parent = null;      //root state has no parent
      Index = -1;        //root didn’t originate from a move
      Depth = 0;         //initial state
}

uniqueNodes.Add(root.Value, root); //root.value is our key

Now let’s simulate our loop of generating a node, check it, and store it if unique, starting from our root node and see how can we further improve our nodes and tree to simplify our task;

We use a non-recursive queue implementation because we know we can be dealing with an enormous number of nodes (our function call stack really didn’t like recursion for millions of nodes)

Queue<Node> queue = new Queue<Node>;   //queue for breadth-first generation
queue.Enqueue(root);                   //we start from our root
 
//the loop
while (queue.Count > 0 ) {      
      Node currentNode = row.Dequeue();      //Get next node in queue.
 
      for (int index = 0; index < 4; index++) { 
            //Given the current parent node and the move, we get the resulting
             //child node value, encoding our game state
             int value = CreateValueFromMove(currentNode, index);
 
             //creation similar to root node but with additional parent and index
             //initialization as now we are generating from an existing node
             Node node = new Node(value) {
                Value = value;     
                State = DeadEnd       //we do not know if we can reach a solution
                Parent = CurrentNode; //set the parent for solution traversal
                Index = index;        //we track the originating move
                Depth = currentNode.Depth + 1;
             }
...
             //we check for winning condition
             If (WinCondition(value)) {
                   EndBranch(value); //Win case, terminate this branch
 
             } 
             else if (!uniqueNodes.ContainsKey(value)) {  //check duplication
                   AddDuplicate(value); //Duplicate case, handle it
             } 
             else { 
                   AddUniqueNode(node); //Unique node case
             }
      } 
}

Let’s examine all our cases’ details, to find out why this idea of a parent-focused tree can help us solve both the winning condition upward propagation and the duplicate node management.

Unique node case

this node state has not been encountered before so we have to add it to our “tree” and save it as unique. This case is the simplest of the 3:

void AddUniqueNode(Node node) {        
      uniques.Add(node.Value, node); //add it to our dictionary, node.Value as key
      queue.Enqueue(node); //enqueue it to continue our generation from this as root
} 

Being in the queue, the generator will continue to generate this unique node 4 children in a later pass as expected.

Win case

void EndBranch(int value) {            
   If IsMaxcombo(value) //check if our win state has the max combo
       currentNode.PropagatestatetoRoot(NodeState.Ok);
   else
       currentNode.PropagateStateToRoot(NodeState.Maxcombo);
}

Depending on the winning condition, we propagate back to our root the correct state, while collecting the reversed steps to reach this winning node. Once we reach our root, we save the solution.

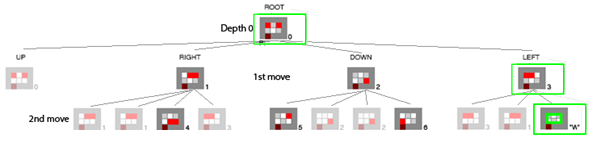
In our level 1-1 example, after our generation reaches the first winning node from S3 (with a Max Combo as both skiddy disappear at the same time), all the nodes highlighted in green will have their corresponding States set to MaxCombo, the others are still all DeadEnds.

Duplicate case

When we encounter a new node which is a duplicate of a previously encountered node, we cannot simply add it to the queue as this will create an infinite loop in our generation, yet we can’t completely discard as this internal loop is necessary to correctly propagate winning conditions to all nodes, otherwise we’ll end up having some false DeadEnds leftover nodes.

This is not visible in level 1-1 because all branches lead to a winning so let’s use a variation to show this situation:

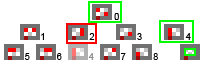S2 can only generate an S4 duplicate going left. Without special consideration, after we discard this duplicate, S2 will remain in DeadEnd state because there are no additional children leading to a winning state.

This is the case where our reversed tree comes into play. Let’s first add another field to our node, an additional list of secondary parent nodes. We will add here all the nodes that generate child which are duplicates of this node and as a result can be considered as additional parents of this node.

// A node contains information about board configuration and relations to other nodes
class Node {
      int Value;         //encodes our pieces’ layout and board score
      NodeState State;   //max-combo, ok or dead-end?
      Node[4] Child;     //the states originating from the next 4 moves
      int Index;         //generating moves(none, up, right, down, left)
                         //                 -1     0   1      2     3
      Node Parent;       //state before last move, used to traverse our solution
      Int Depth;         //how many moves it took to reach this node
      List<Node> Parents; //secondary parents from node duplication
}

This is why we call this a “reversed tree”, because without child but with the secondary parents, the relationship between our nodes is expressed like the following example for level 1-1

Node relationship expressed as a “reversed tree”, there is no need to represent win nodes.

Note: it’s possible also for our root node to receive some secondary parents during generation, in level 1-1 it just doesn’t happen.

Now when we encounter a duplicated node that we do not enqueue, we find the original existing node in our unique nodes dictionary, then we add the current parent node to the secondary parents of the original node. In level 1-1 above, S1 has S0 has an original parent, but when we reach its duplicate from S3, we just add S3 in s1 parents list. We do the same when we reach S3 from S1.

In pseudo-code:

void AddDuplicate(int value) {
      Node node = uniques[value];      //find the original node in our dictionary
      node.InsertParent(currentNode);  //add the new parent as a secondary
      ...
}

And, in case the original node state is already set to Ok or MaxCombo from a previous win, we immediately propagate this condition from the current parent up to the root, because the du