Part 1

Introduction

It is said that the best suggestion on learning how to make video games is to go and make one. So we did. We started with a simple idea, with the main goal of developing a complete, interesting game while learning along the way and this is a kind of “post-mortem” developer diary on the challenges we faced and how we managed to solve them.

It will be an in-depth feature on our procedural level generation, analysis, and rating and will act as a companion piece to talks given at Codemotion 2012 in Rome (http://roma2012.codemotion.it/talk/skiddy-esperienza-un-primo-progetto-serio-nel-mondo-dei-videogiochi/index.html) and at Politecnico di Milano on October 31^st, 2014 (https://www.youtube.com/watch?v=8_UeywA68kA).

Those talks were design/gameplay oriented but they already presented a brief overview of our level creation system and tools.

Game Mechanics

Skiddy is a puzzle game where the aim is to lead all colored creatures to the matching color goal and clear the level. User input will move all non-static elements in any of the four directions until any obstacle is hit or according to their characteristics. Their movement cannot be altered while in motion.

Levels are composed of different block types laid out on grids of 5x4 to 8x7 cells.             

The outer border can only contain solid, unmovable Blocks, and Goals; the inner area of 3x2 to 6x5 can be filled with any other block except Goals.

Some of our available block types, grouped into 2 main categories:

Statics (they do not move regardless of input or other blocks interactions)

Moveable (they move either by player input or by interacting with other blocks)

All adjacent Skiddies will clear out in a combo when touching a goal.

3 Special medals are awarded for clearing a level in a set minimum number of moves (par), by completely clearing each color in a single move (max combo) or doing both at the same time (perfect!).

Hand-made levels

Initially Christian, the game designer, was plotting the first test levels by hand to define block behavior, interaction, goal conditions, and difficulty.

But while small levels with few blocks could still be completely reproduced on paper and solved with the mind, it was quickly apparent that the complexity was going to skyrocket on the way to define the 100 and more levels required for the easy game mode, and even worse for the hard mode.

We had no choice but to try to implement a tool to help us design, solve and analyze levels.

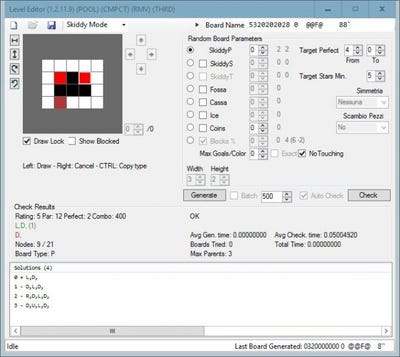
But what will be the limit of this tool? And can the tool tell us if a level is not only correct, but also good? What are the traits of a good level? Here’s how we found out.

Complexity problem

For the intent and purpose of level generation and analysis, blocks mechanics, once implemented correctly, are not important as long as it is understood that player input will take an existing board state and output a resulting state, with the game acting as a black box in the middle. This turns our game into a deterministic state machine with only 4 possible input (up, right, down, left), and a finite number of states S?

         player           block 
         input          mechanics
   S0    ------> [GAME] --------->    S?
Starting                           Resulting
 state                               state

Where:

S? == S0 if the received input will not change the level state.

S? == Sn if it’s a new, unique node.

S? == Sn’ if the resulting state was already created in a previous move.

As static blocks never change, each state S? is determined by the position of all the moveable blocks.

To verify that a level allows all winning conditions for the 3 medals to be obtainable, we also need to keep track of other information describing the game state at each Sn. Is this a Win state (all Skiddies cleared)? Is this a Combo state (always cleared each color in a single move)? And other conditions that will emerge later on, related to a level quality rating.

Even small levels can generate a lot of possible valid S? states, and the addition of a single piece can increase the complexity exponentially.

Level 1-1 in the game and its block representation: 3x2 moveable area. 2 Red Skiddies, 4 Empty Blocks, 1 Red Goal. This simple level contains the minimum number of blocks to fully show basic mechanics and allows one to gain all 3 medals.

Before we even start to think how to track these states, can we get an idea of how many states there will be in a level just looking at the available blocks? Statistics to the rescue!

This problem is a special case of distinguishable permutations of n objects, of which:

and the result is r = n!/n1!n2!n3!…nk! (the factorial of the total blocks divided by the product of the factorials of each type quantity).

In our case: n1==2; n2==4; r0 = (2+4)!/2!*4! == 6!/2*24 == 720/48 = 15

But this only gives us the result when BOTH red blocks are still in play, we must also consider the situation of a single block being cleared while the other remains in play! So we repeat the same formula for:

n1==1; n2==5; r1 = (1+5)!/1!*5! == 6!/1*120 == 720/120 = 6

And the final result is r01+r1 = 21

So a generalized formula for Skiddy becomes the sum of distinguishable permutations of n objects, where the distribution in n1 to nk must account for each block type (red, yellows, ice, etc..) to go from their starting quantity to 0;

In a 3x3 level with 2 couples of different colored Skiddies and 4 free blocks for example we have to calculate distinguishable permutations for

 n1 n2 n3
2  2  4    r0 = 420
2  1  5    r1 = 168
1  2  5    r2 = 168
2  0  6    r3 =  28
0  2  6    r4 =  28
1  1  6    r5 =  56
1  0  7    r6 =   8     
0  1  7    r7 =   8
r0 + r1 + …. + … r8  =  884 

but in the above level, possible game states are only 82.

Luckily this is only a theoretical ceiling, because game rules will not allow the generation of all these states, but we can get an interesting relation between potential complexity and real complexity.